でんきの「で」超入門編1
社会人になってから、もう一回電気を勉強したい。それも実践的に。
回路設計もしてみたい。電気工事の資格が欲しい。
そんな方が、この電気の世界に入りやすいように書いてみます。
電気関係の教科書は難しい。
いきなり公式とか出てきて覚えられない。
そんな心配はいりません。
電気の世界では、覚えるということがほとんどありません。
感覚的に理解(経験)すること。理由を考えることが大切です。
最低限必要な知識
というわけで、まずは最低限必要な知識です。
逆に言えば、これさえ知っていれば、ほぼ日常的に困ることはありません。
いずれも、義務教育で習う範囲です。
オームの法則
E(電圧)[V] = I(電流)[A] x R抵抗値[Ω]
電力の計算
P(電力)[W] = E(電圧)[V] x I(電流)[A]
補助単位
1/1000 = m(ミリ)
x1000 = K(キロ)
など。普通の算数と一緒です。
某キャリアがデータサイズを G(ギガ) なんて呼んでますが、これも補助単位(1,000,000,000倍)です。この場合の実際の単位は Byte(バイト)。
こういう輩が電気への苦手意識を一般の人に植え付けていきます。
エネルギー保存の法則
例えば同じ60[W]の電球でも、
LED > 蛍光管 > 白熱球
の順に明るいのですが、消費電力はいずれも同じです。
では、光になれなかったエネルギーはどうなるかというと、「熱」になります。
つまり、同様に60[W]の電球の発熱量は
白熱球 > 蛍光管 > LED
になります。トータルで60[W]になるわけです。
部品や配線にはすべて抵抗成分がある
電気が電線や部品を通ると、抵抗成分によって通った後の電圧は下がっています。
これは、すべての部品についてあてはまります。
そして、その電圧低下した分のエネルギーは熱になります。
微分と積分について
微分、積分は高校数学で習いますね。
もちろん数学なので数式で証明されなければならず、これがものすごく難しい印象が残っている人も多いと思いますが、ざっくり以下の理解があれば、電気の世界ではとりあえず大丈夫です。
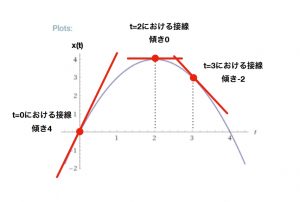
微分
曲線の瞬間的な傾き。
曲線といえどもx-yのグラフであり、ごくごく小さな時間に区切っていくと、その瞬間の傾きを直線で表すことができるということ。
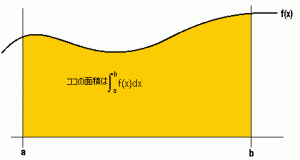
積分
曲線に囲まれた部分の面積。
面積は即ちエネルギーの大きさを表し、面積が大きいほどエネルギーが大きい。
エネルギーの大きさは、瞬時のエネルギー(Y軸)と時間(X軸)を合わせたものです。
参考
https://math-fun.net/20180704/132/
http://proofcafe.org/k27c8/math/math/analysisI/page/find_floor_space_in_graph/